Quand on débute en électronique, que ce soit avec un Raspberry Pi ou un Arduino, on se trouve rapidement confronté au calcul des résistances. Que ce soit pour alimenter une LED, polariser un transistor ou autre… on a toujours besoin de faire un calcul.
Manu, un fidèle lecteur (et intervenant) du blog et du forum a concocté cette Pi-ramide qui vous rappellera « sur le pouce » les formules dont vous avez besoin.
Cliquez pour obtenir une information sur les niveaux.
Au sommaire :
Une Pi-ramide pour des équations d’électricité
Si certains pensent que les Égyptiens de l’antiquité connaissaient l’électricité, c’est surtout leurs connaissances en géométrie que l’on retrouve dans la construction des pyramides.
C’est ce solide que Manu a retenu pour créer un aide mémoire à l’usage des électroniciens débutants.
Comment ça marche ?
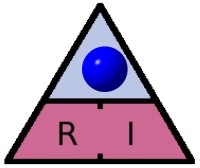
C’est tout simple ! On va prendre un exemple…
 |
On fait simple, hein ! On applique une tension U aux bornes d’une résistance. Cette tension fait circuler un courant I dans la résistance. |
 |
Prenons ce triangle qui comporte les lettres U, R et I
|
 |
Vous connaissez la résistance : R = 100 Ω et vous avez mesuré le courant : 50 mA (0,050 A) Vous voulez connaître la tension aux bornes de la résistance ? Pour trouver la formule, posez le pouce sur la valeur que vous cherchez (posez le pouce sur U) Il ne reste que les 2 lettres du bas : R et I qui sont l’une à côté de l’autre… la formule est U = R x I U = 100 x 0.050 = 5 VAllez une autre application : |
 Vous branchez une LED en sortie de GPIO sur un Raspberry Pi (vous avez de ces idées, aussi 😉 ). Lorsque la tension du GPIO passe à 3,3 volts (état 1) la LED s’éclaire. La tension à ses bornes et de 1,6 volts (vous l’avez mesurée ou mieux vous avez lu la doc – nan, là je rêve 😀 ) et un courant de 10 mA (0,010 A) parcourt la LED (ça aussi c’est dans la doc (là, j’insiste 😉 )Quelle résistance devez vous utiliser pour que la LED éclaire normalement, sans se transformer en morceau de charbon ? |
|
 |
Bon, comme on cherche la valeur de R c’est sur cette lettre qu’on va poser le pouce… Il nous reste U en haut du triangle et I en bas… Voilà notre formule. R = U / I Vous allez me dire je ne connais pas U, la tension présente aux bornes de la résistance ! Il y a 3,3 volts sur une de ses pattes et 1,6 volts sur l’autre patte… Donc entre les 2 il y a ??? 1,7 volts (ne me dites pas que vous avez sorti la calculatrice 🙁 )Allez on calcule R = 1,7 / 0,010 = 170 Ω Zut il n’y en a pas dans ma boîte ! bah mettez 180 Ω ou 150 Ω et ne dites rien à personne, ça va fonctionner 🙂 |
| De la même façon, si vous cherchez à trouver I, mettez le pouce dessus et il reste ?
fastoche : I = U / R |
 |
C’est tout pareil !
Toutes les faces de la pyramide fonctionnent de la même façon !
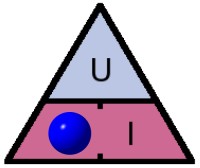
Ici on voit à droite P et R ainsi que I2 : P c’est la puissance en watts, R et I on les a vus juste avant.
Alors quelle doit être la puissance de la résistance dans l’exemple précédent ? (c’est pour éviter qu’elle n’émette des signaux de fumée avant de rendre l’âme)
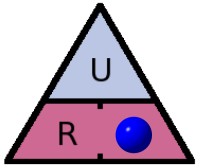
Je cherche P => je mets le pouce dessus il reste ??? R x I2
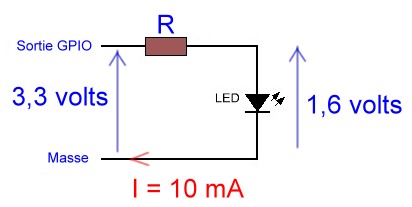
R on a dit 180 Ω (c’est celle que j’avais en stock) et un courant de 10 mA (0,010 A) =>
P = 180 x 0,01 x 0,01 = 0,018 watt
Pas de souci une résistance 1/4 watt (250 mW) fera l’affaire puisque la puissance dissipée n’est que de 18 mW. Par sécurité prévoyez toujours une puissance au moins double de la puissance nécessaire.
Et en fonction de la face que vous choisissez, vous avez une de ces 4 formules :
- P = U x I
- U = R x I
- P = R x I²
- P = U² / R
Et le carré en dessous de la Pi-ramide ?
Ah oui c’est vrai il y a un carré sous la Pi-ramide ! J’ai failli oublier de vous en parler 🙂
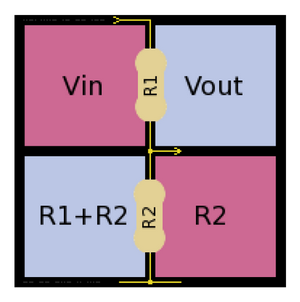
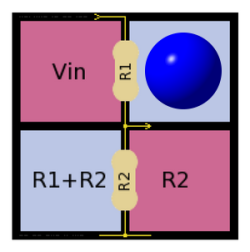
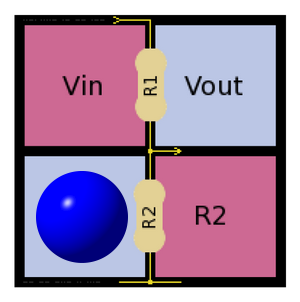
Celui-là concerne le pont diviseur de tension :
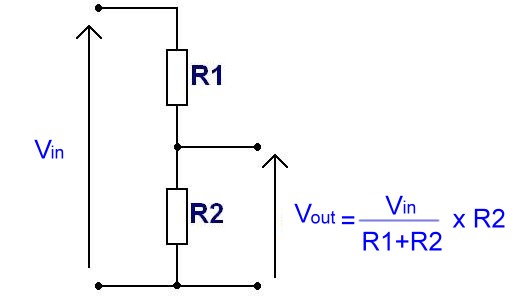
Une tension d’entrée Vin est appliquée au pont diviseur constitué par 2 résistances, R1 et R2. Il permet de récupérer en sortie Vout, qui est une partie de la tension d’entrée.
 |
Bon allez on cherche Vout donc… on met le pouce dessus ! On multiplie ce qui est en diagonale et on divise par ce qui reste ! Vout = (Vin x R2) / (R1+R2) On voit tout de suite que si R1=R2… |
Exemple de pont diviseur
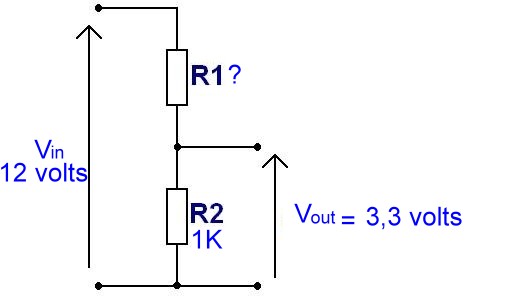Bon, cette fois on a un capteur (de ce que vous voulez 🙂 ) qui sort soit rien (0 volt) soit du 12 volts (niveau 1). On ne peut pas envoyer sa sortie sur un port GPIO du Raspberry Pi. Un GPIO supporte au maximum 3,3 volts !
On va utiliser un pont diviseur pour ramener la tension d’entrée (12 volts) à 3,3 volts. J’avais en stock une résistance de 1KΩ qui fera l’affaire pour R2. Bon, et je mets quoi pour R1 ???
 |
Zut sur le carré il n’y a pas R1… Juste R1+R2 ! Allez on masque R1+R2, c’est ce qu’on cherche (si on connait R1 + R2 on connait R1, non ?)
On multiplie la diagonale et on divise par ce qui reste ! (R1 + R2) = (Vin x R2) / Vout (R1 + R2) = (12 x 1000) / 3,3 (R1 + R2) = 3636 Ω Ça j’ai pas en stock : j’ai 2,7KΩ et 2,2KΩ dans ma boîte… Je prends laquelle ? |
Bin… pour vérifier on va faire le calcul dans l’autre sens si vous voulez bien ! reprenez le pont diviseur vu précédemment avec
R2 = 1KΩ et R1 = 2.7 KΩ
Je vous laisse faire le calcul… on trouve Vout = 3,24 volts
ensuite on prend R2 = 1KΩ et R1 = 2.2 KΩ
on refait le calcul et on trouve Vout = 3,75 volts
Alors vous prenez quoi, vous ?
tadaaaa ! Moi je prendrai R1 = 2.7 KΩ car la tension de 3,24 volts est compatible avec les ports GPIO vu qu’elle est inférieure (très peu) à 3,3 volts.
Si je mets la résistance de 2,2 KΩ, la tension de 3,75 volts va dépasser la limite de 3,3 volts et mon port GPIO risque d’être détruit, si je n’ai pas de bol c’est le CPU qui va cesser de fonctionner… Et un Raspberry Pi sans microprocesseur c’est ??? Bon à mettre à la poubelle (pensez au recyclage ! )
Les puristes vous diront que ce n’est pas bien d’abaisser la tension avec un pont diviseur pour attaquer un GPIO. Ils vous recommanderons d’utiliser un convertisseur de tension, beaucoup plus sûr. Ils ont raison !! Mais le pont diviseur fonctionne très bien si vous êtes certain(e) de la tension du capteur.
Retenez la méthode qui consiste à refaire le calcul « dans l’autre sens ». Ça permet de s’assurer que la valeur trouvée est cohérente et que les calculs son justes.
Un exercice pour voir si vous avez compris
Pour finir je vous propose un exercice pour voir si vous arrivez à vous débrouiller… (attention il y a peut-être un piège 🙂 … ou pas) :
Vous avez un pont diviseur constitué de 2 résistances R1 = 2,2 KΩ et R2 = 5,6 KΩ. La tension de sortie Vout doit être de 5 volts… Vous envoyez combien sur Vin ?
Prenez votre temps, faites votre calcul, vérifiez en refaisant le calcul « à l’envers ». Quand vous serez certain(e) que votre résultat est bon, ouvrez ce PDF qui vous propose la solution 🙂
Comment réaliser cette pyramide ?
Méthode 1 : couper-coller
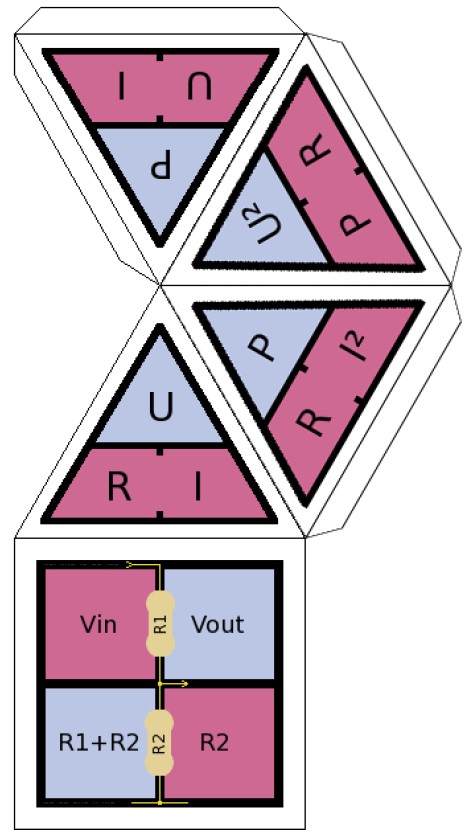Manu vous facilite la tâche : il a réalisé un modèle de pyramide que vous pouvez découper. C’est celui que j’ai utilisé. Il y a même les rabats pour le collage. Téléchargez ce fichier PDF et imprimez le.
Méthode 2 : Le Python
Pour ceux qui voudraient fabriquer leur propre Pi-ramide, Manu a écrit un programme Python qui calcule les différentes dimensions de l’objet :
#!/usr/bin/python2.6
# -*- coding: utf-8 -*-
def Pythagore (a,b,c):
#=============
# Affiche la valeur des côtés du triangle rectangle
# a et b sont les côtés adjacent à l'angle droit
# c est le côté opposé à l'angle droit, l'hypoténuse
#=============
print " a = %s \n b = %s \n c = %s" % ( str(a), str(b), str(c) )
#=============
# "a" est la valeur à chercher
#=============
if type(a) == type('str'):
a = ( c**2 - b**2 ) ** .5
print "a = %f \n" % a
return a
#=============
# "b" est la valeur à chercher
#=============
if type(b) == type('str'):
b = ( c**2 - a**2 ) ** .5
print "b = %f \n" % b
return b
#=============
# "c" est la valeur à chercher 'hypoténuse'
#=============
if type(c) == type('str'):
c = ( a**2 + b**2 ) ** .5
print "c = %f \n" % c
return c
#
# Valeurs des côtés de la pyramide
#
cote_base = 10 # base en carré
cote_base_sommet = 10 # arrêtes vers le sommet
#
# Longueur de la diagonale sur la base
#
print "\nDiagonale base :"
diagonale_base = Pythagore ( cote_base , cote_base , "?" )
#
# Centre pyramide par rapport à la diagonale base
#
print "\nCentre de la pyramide sur la diagonale :"
centre_hauteur_diagonale = diagonale_base / 2
print centre_hauteur_diagonale
#
# Hauteur de la pyramide
#
print "\nHauteur de la pyramide :"
hauteur_pyramide = Pythagore ( "?" , centre_hauteur_diagonale , cote_base_sommet )
#
# Centre pyramide par rapport à un côté de la surface de base
#
print "\nCentre de la pyramide sur le coté :"
centre_hauteur_cote = cote_base / 2
print centre_hauteur_cote
#
# Hauteur sur face incliné de la pyramide
#
print "\nhauteur sur plan face incliné :"
hauteur_face_incline = Pythagore ( centre_hauteur_cote , hauteur_pyramide , "?")
Conclusion
Avec la Pi-ramide de « Tout en carton » sur votre établi, finis les oublis de formule. C’est un outil que vous pouvez laisser traîner sans crainte des court-circuits ou de l’usure des batteries…
Un jour vous n’en aurez plus besoin. Vous aurez intégré ces formules. Mais vous vous souviendrez de cette Pi-ramide qui vous a aidé à démarrer 🙂
Cet article ne tient pas compte des résistances présentes en parallèle sur l’entrée ou la sortie du pont… C’est une autre histoire 😉
Bonjour François ,
Merci pour la publication de cet article et la mise en forme pour les explications .
Quelques point à rajouter niveau explication :
1°)
Déjà , le pont diviseur , comme son nom l’indque , ne sert qu’à convertir des tension dans un seul sens , Vin vers Vout et pas dans l’autre sens , on ne fera jamais du 12V à partir du 5V avec ce type de montage .
Il sert surtout à donner une information en tension (U) pour les signaux d’entrée et dont le courant (i) est très faible voir négligeable .
Il n’est par recommandé pour alimenter en puissance (I important) un montage comme le ferait plus efficacement un régulateur de tension .
Le principe du calcul sur la face carré de la pyramide est le suivant :
Dans un montage en série , le courant qui traverse chaque composant est stictement identique .
Le fait de venir prendre une mesure en tension au borne d’un des composants , implisque que le courant consommé par cette dérivation soit le plus faible possible voir négligeable afin de préserver cet équilibre .
Dans ces condition , on a trois formule pour chaque résistance et l’ensemble du montage :
I = U1 / R1
I = U2 / R2
I = Vin / (R1+ R2)
Rappel : Vin = U1 + U2
Comme i est quasiment identique , on peut mettre en relation directe les élémente suivants
U1 / R1 = U2 / R2
ou
Vin / (R1+R2) = U2 / R2
U2 est nomé sur le pont diviseur Vout .
2°)
En mathématique , il y a plusieur façon d’écriture un même calcul .
U = R x I
U = R.I
U = Ri
Donc quand on lit le calul à faire avec deux élément côte à côte (face triangulaires) , c’est forcément une multiplication .
Dès que l’une des deux valeur est « sur » l’autre , c’est une division .
R = U / I
R = U « sur » I
…… voir point 1°) ….
Ui « sur » R1 = U2 « sur » R2
Vin « sur » (R1+R2) = Vout « sur » R2
3°)
Dans le programme , certains seront surpris de voir les calculs de Pythagore sans la fameuse fonction SQR (SQuare Root) = Racine carré en français .
Rappel du théorème de Pythagore : c² = a² + b²
« c » étant la diagonale (hypoténuse) du triangle rectangle .
Cette fonction SQR peut être remplacé par la puissance 1/2 ou puissance 0,5 .
soit : c = SQR (a² + b²)
est identique à : c = (a^2 + b^2) ^0.5
en python ça s’écrira : c = ( a**2 + b**2) **0.5
Lancer Python et tapez ce qui suit :
9**0.5
on obtient bien 3.0 et 3 x 3 = 9
J’en dit pas plus sinon je vais me faire couper .
Tant pis pour l’antibavard du blog …. Hi !
Pour ceux qui veulent construire leur propre Pi-Ramide à taille différente à l’aide d’un compas , il y a cette méthode :
http://fr.wikihow.com/dessiner-un-hexagone
Il ne retera qu’à relier d’un trait tous les sommets de l’hexagone et éliminer 2 triangles sur les 6 , en prenant soin de laisser des languettes pour l’assemblage , puis dessiner le carré de la base de la Pi-ramide .
salut pour une belle pyramide
polyhedron(
points=[ [115,115,0],[115,-115,0],[-115,-115,0],[-115,115,0], [0,0,147] ],
faces=[ [0,1,4],[1,2,4],[2,3,4],[3,0,4], [1,0,3],[2,1,3] ] );
le programme python c est pour une imprimante un navigateur web?
Bonjour cortomaltese77
C’est pour avoir des dimensions pour la construction en objet réel .
Les deux variable à changer sont à la ligne 35 et 36 , mais il faut qu’elles soient identique sinon les triangles ne seront plus équilatéraux et ça change tout à la construction .
Le programme python est à copier dans un fichier avec l’extension « .py » . ex: : test.py
Il se lance avec la commande suivante dans une fenêtre console en prenant soint d’être dans le dossier où se trouve le fichier à exécuter .
python test.py
Il a été écrit en python version 2.6 , il est fort possible que des modifications soient à faire si on utilise une version de python plus récente en 3.x .
Si vous avez des idées pour créer une pyramide virtuelle en 3D avec mapping , ça peut aussi être intéressant pour ceux qui ont des difficultés avec des ciseaux et de la colle (ou de l’alcool aussi) .
Pour imprimer la Pi-ramide avec les formules tout près , juste à découper et à coller , il faut suivre le lien indiqué par François .
https://www.framboise314.fr/wp-content/uploads/2017/01/Pyramide-des-formules-electricit%C3%A9.pdf
Il s’agit d’un fichier PDF à télécharger et à imprimer .
En fait , ce mémo en 3 dimensions remplace avantageusement un autre mémo certes moins encombrant mais plus dificile à retrouver sur un bureau désordonné et moins pratique à utiliser pour un débutant .
http://www.e-genieclimatique.com/wordpress/wp-content/uploads/2012/04/Formule_de_base_electrique_avec_U_R_I_P.jpg
C’est juste génial comme idée ce truc 🙂
Je pense que je n’en n’ai pas besoin car un peu trop rodé avec mes formules.. mais que ça en aidra plus d’un 🙂
re ,désolez j’avais mal compris le programme pyton j ai cru qu’il gênerai le patron du dessin (il a été fait avec quelle logicielle?)
j etait partit sur fichier pour une machine CNC ou imprimante 3d
openscad pour la pyramide il manque le rapport avec Pi et le nombre d or ?14/11 pour khéops
la pyramide du fichier
polyhedron(
points=[ [52,52,0],[52,-52,0],[-52,-52,0],[-52,52,0], [0,0,66] ],
faces=[ [0,1,4],[1,2,4],[2,3,4],[3,0,4], [1,0,3],[2,1,3] ] );
pour graver les symboles c’est plus compliquer peut être passer par Inkscape et une Extensions pour convertir un dessin vectoriel en un objet utilisable par OpenSCAD (https://github.com/l0b0/paths2openscad) et touts assemblée dans freecad
Bonjour ,
Le logiciel de dessin utilisé est GIMP sous Linux , c’est l’équivalent de Photoshop sous windows .
Il n’a pas , à ma connaissance , de facilités pour construire des volumes comme cette pyramide .
J’ai donc dû calculer toutes les côtes et angles et les dessiner à la main pour que celle ci soit la plus simple à reproduire .
Malgrès cela et sur les conseil de François , j’ai édité une version toute prête à imprimer en PDF qui évite tous ces calculs .
A l’origine , je voulais respecter les proportions et tout et tout des vrai pyramides , mais j’ai vite déchanté surtout au moment de coller les images des formules , avec la rotation , ça altère beaucoup l’image .
Je me suis contenté de faire des triangles équilatéraux , ce qui est beaucoup plus simple à construire à partir d’un simple hexagone , puis de coller un carré .
Reste plus que les languettes à ajouter .
Les images sont tournés de 60° , 120° et 180° , ce qui altère moins l’image .
Le modèle de pyramide 3d donc je te parlais , ça serait un modèle en imagerie virtuelle 3D qui pourrait rester dans le Raspberry Pi et qu’on pourrait appeler et faire tourner à sa convenance ; pas une construction en imprimante 3D , ça serait beaucoup trop compliqué .
Peut-être avec ton idée sur OpenCAD .
Sur l’idée de la Pi-ramide (des formules), toute en papier , je prévois d’en construire une toute en carton qui servira de boitier économique au Raspberry PI .
A suivre ….